
Researchers uncover the mathematical construction behind mesmerizing tiling patterns, linking their visible enchantment to the complexity of mathematical analysis.
In a brand new examine, mathematicians at Freie Universität Berlin present that planar tiling, also called tessellation, is excess of an ornamental association of shapes.
Tessellations cowl a floor utterly with repeating geometric kinds, with out gaps or overlaps, and the researchers reveal that these constructions also can function highly effective instruments for tackling troublesome mathematical issues. The examine, performed by Heinrich Begehr and Dajiang Wang, was printed within the journal Relevant Evaluation. The work brings collectively concepts from advanced evaluation, partial differential equations, and geometric operate concept.
A key idea explored within the examine is the “parqueting-reflection precept.” This technique entails repeatedly reflecting geometric shapes throughout their edges to fill a aircraft, creating extremely symmetric patterns.
Such tessellations are visually acquainted from the art work of M.C. Escher, however the researchers present that the precept has far-reaching mathematical worth. Particularly, it gives a scientific technique to strategy classical boundary worth issues, together with the Dirichlet and Neumann issues, which come up incessantly in mathematical physics.
“Our analysis reveals that magnificence in arithmetic just isn’t solely an aesthetic notion, however one thing with structural depth and effectivity,” says Professor Heinrich Begehr. “Whereas earlier analysis on tessellations has targeted largely on how shapes can be utilized to tile or cowl a floor – for instance, some well-known work carried out by Nobel Prize winner Sir Roger Penrose – utilizing the parqueting-reflection technique to generate new tessellations opens up new prospects. It’s a sensible software for creating methods of representing features inside these tiled areas, which might be helpful in areas reminiscent of mathematical physics and engineering.”
One necessary end result of this strategy is the flexibility to derive express formulation for kernel features, together with Inexperienced, Neumann, and Schwarz kernels. These mathematical instruments play a central position in fixing boundary worth issues encountered in physics and engineering. On this manner, the examine forges a transparent hyperlink between geometric instinct and rigorous analytical strategies.
Curiosity within the parqueting-reflection precept has grown steadily over the previous decade, significantly amongst early-career researchers. For the reason that idea was first developed, it has been the topic of fifteen dissertations and closing theses at Freie Universität Berlin, in addition to seven extra doctoral dissertations accomplished by researchers at establishments overseas.
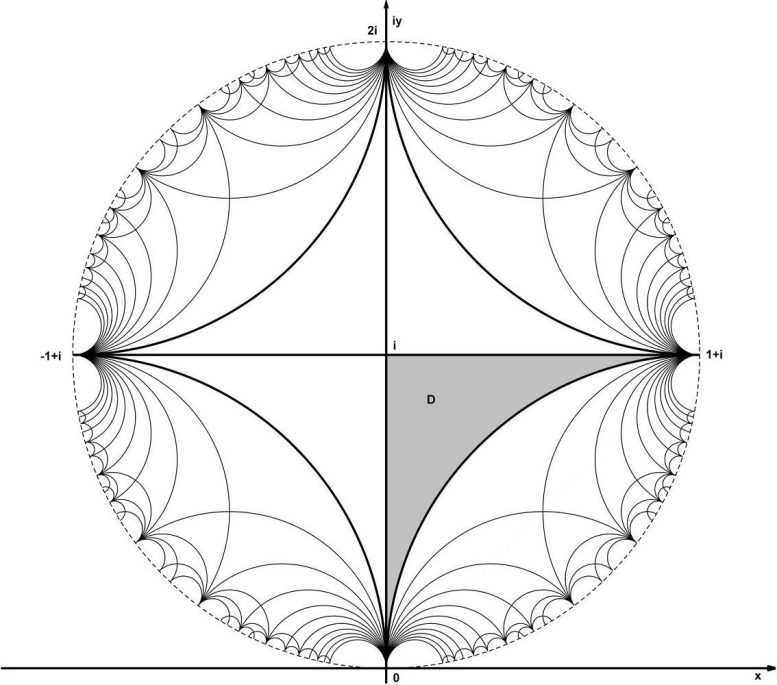
Remarkably, the precept works not solely in Euclidean house, but in addition in hyperbolic geometries – the sorts utilized in theoretical physics and fashionable visualizations of spacetime. Curiosity within the precept stays excessive. Final yr, Begehr printed an article, “Hyperbolic Tessellation: Harmonic Inexperienced Operate for a Schweikart Triangle in Hyperbolic Geometry,” within the journal Complicated Variables and Elliptic Equations, wherein he demonstrated using the parqueting-reflection precept to assemble the harmonic Inexperienced operate for a Schweikart triangle within the hyperbolic aircraft.
“We hope that our outcomes will resonate not solely in pure arithmetic and mathematical physics,” Dajiang Wang says, “however could even encourage concepts in fields like structure or pc graphics.”
The Tiling Custom in Berlin
For practically 20 years, the analysis group led by Heinrich Begehr at Freie Universität Berlin’s Institute of Arithmetic has been learning what are generally known as the “Berlin mirror tilings” – a technique based mostly on the unified reflection precept developed by Berlin-based mathematician Hermann Amandus Schwarz (1843‒1921).
On this strategy, a round polygon – a form whose edges include items from straight strains and round arcs – is mirrored repeatedly till all the aircraft is seamlessly and utterly tiled, with none overlaps or gaps. These patterns are usually not solely visually putting but in addition allow express integral representations of features – a key software for fixing advanced boundary worth issues.
“Mathematicians as soon as had to make use of a three-part self-importance mirror to provide an limitless sequence of photos,” says Begehr. “These days, we will use iterative pc packages to generate the identical impact – and we will complement this with precise mathematical formulation utilized in advanced evaluation.”
Schweikart Triangles and Hyperbolic Magnificence
Whereas they’re thought-about very aesthetically spectacular, tessellations in hyperbolic areas – for instance, inside a round disc – characterize a specific problem for mathematicians. That is the place “Schweikart triangles” come into play: particular triangles that includes one proper angle and two zero angles, named after newbie mathematician and legislation professor Ferdinand Kurt Schweikart (1780‒1857).
These triangles allow the whole, common tiling of a round disc – producing patterns with an aesthetic enchantment that gives contemporary inspiration for pc graphics artists and designers alike. On the similar time, the underlying mathematical constructions are extremely advanced and require superior analytical strategies.
Arithmetic as a Visible Science
The findings of the crew spotlight an typically ignored side of arithmetic: it isn’t solely an summary self-discipline, but in addition a visible science – one wherein construction, symmetry, and aesthetics play a central position. When paired with fashionable visualization strategies, graphics software program, and digital instruments, these insights change into all of the extra related.
References:
“Magnificence in/of arithmetic: tessellations and their formulation” by H. Begehr and D. Wang, 13 June 2025, Relevant Evaluation.
DOI: 10.1080/00036811.2025.2510472
“Hyperbolic tessellation: harmonic Inexperienced operate for a Schweikart triangle in hyperbolic geometry” by Heinrich Begehr, 15 October 2024, Complicated Variables and Elliptic Equations.
DOI: 10.1080/17476933.2024.2408729
By no means miss a breakthrough: Join the SciTechDaily newsletter.
Observe us on Google and Google News.
















